서 론
Body Mass Index (BMI)는 체중인 Weight (W)를 신장 Height (H)의 제곱으로 나눈 값으로 간단하게 과체중과 비만을 판정하는 지수이며 이는 Adolphe Quetelet에 의해 고안되어 Quetelet’ s Index라고도 불린다.
1832년, Adolphe Quetelet에 의해 제안된 W (kg)/H2 (m2)의 BMI는 비만판정을 위한 지수가 아닌 ‘보통 체중’을 판정하기 위한 방법에서 출발하였다[1]. 기존의 상대체중을 표현하는 W (kg)/H (m)의 지수는 모든 사람들이 1 m라는 가정하에 표준체중을 구하는 방법으로 이해될 수 있지만 높은 신장을 가질수록 지수의 평균 값이 증가하는 양상을 보여 ‘보통 체중’의 판정을 위한 표준화 과정에 어려움을 보였다[2]. 이에 Quetelet은 성인의 낮은 신장집단의 신장을 t, 높은 신장집단의 신장을 T로 가정하고 낮은 신장집단의 표준체중을 p, 높은 신장집단의 표준체중을 P라고 가정했을 때 t:T는 5:6의 비율을 보이고 p/t:P/T또한 5:6의 비율임을 확인했다. 이는 다시 말해 t:T의 비율과 p/t:P/T의 비율이 같아 p/t2과 P/T2의 비가 1:1임을 알 수 있고 이 방법을 통해 작은 신장집단과 높은 신장집단에서 모두 표준화가 가능한 지수인 W (kg)/H2 (m2)을 제안할 수 있었다[2].
3차원 공간에서 존재하는 체중이 W (kg)/H (m)와 같은 1차원적인 지수에 의해 표준화되어야 하는지에 대한 의견은[3], 같은 체형을 가지며 다른 신장을 가진 두 개인의 체중이 신장의 세제곱에 비례한다는 사실과 함께 1897년, Livi [4]에 의해 H (m)/W1/3 (kg1/3)의 형태인 Ponderal Index (PI)가 제안되었다. 이후 1921년, Rohrer [5]는 PI의 다른 형태인 W (kg)/H3 (m3)를 제시하였고 오늘날 이를 Ponderal Index로 지칭하고 있다[6].
이러한 상대체중지수는 모든 사람이 같은 신장을 가졌다는 가정 하의 체중을 나타내기 위한 표준체중공식에 가깝기 때문에 선행연구[7]에서는 다음과 같은 기준이 제시된다. 첫째, 지수는 체중과 높은 상관을 보여야한다. 둘째, 지수는 신장과는 독립적이어야 한다. 이는 다양한 신장으로 이루어진 특정 집단의 사람들이 모두 표준체중을 가진다면 같은 상대체중지수의 값을 가져야 하기 때문이다.
20세기 중반, W (kg)/H (m), W (Kg)/H2 (m2), W (kg)/H3 (m3)과 같은 다양한 지수들 중 ‘비만척도’, 혹은 ‘표준체중’으로 가장 적절한 지수를 찾기 위한 다수의 연구들이 진행되었다. Billewicz et al. [8], Khosla & Lowe [7], Florey [6], Keys et al. [3]의 연구들은 위의 3가지 지수들 중 비만척도로 사용하기 가장 적절한 지수로 현재 BMI로 널리 쓰이는 W (kg)/H2 (m2) 지수를 선택하였다. 그 이유는 체중과 높은 상관을 보이고, 세 가지 지수들 중 신장에 영향을 가장 적게 받아 모든 신장에서 동일하게 사용될 수 있기 때문이었다. 하지만 이러한 연구들은 대부분 남성들을 위주로 진행된 연구였고 Florey의 연구에서만 여성의 경우 W (kg)/H (m) 지수가 신장과의 상관이 더 낮기 때문에 척도로서 더 적합하다는 의견을 제시하였다.
오늘날 흔히 사용하는 상대체중지수의 비만척도 역할은 상대체중지수와 체지방률의 높은 상관관계와 연관이 있다. Flegal et al. [9]의 연구에 의하면 BMI와 DXA scan을 이용해 측정된 체지방률의 상관관계는 20-39세 남성 2,669명(r=0.789, p <.05)과 여성 2,338명(r=0.839, p < .05)에서 높은 상관관계를 보였고, Ranasinghe et al. [10]의 18세 이상 남성 547명과 여성 567명을 대상으로 한 연구에 의하면 BMI와 생체전기임피던스법(Bioelectrical Impedance Analysis, BIA)을 이용해 측정된 체지방률 또한 남성(r=0.75, p <.01)과 여성(r=0.82, p <.01) 모두 높은 상관관계를 보였다. 이와 같은 연구결과는 BMI가 현재까지 개인의 비만을 판정하는 방법으로 사용되는 것의 타당함을 뒷받침하는 것으로 보인다. 하지만 상대체중지수는 모두 체지방을 측정하기 부족하고[6] 신장과 체중 측정에 근거한 BMI는 근육과 지방의 비율, 뼈 구조를 고려하지 않기 때문에[7,11], 이는 비만판정보다 신장이 다른 개인들의 체중표준화과정이라고 보는 것이 더 적절할 것이다. 현재 Asia-Pacific 지역의 BMI 과체중 기준은 23-24.9 kg/m2, 비만은 25 kg/m2 이상으로 분류되고[12], World Health Organization의 과체중 기준은 25-29.9 kg/m2, 비만의 경우 30 kg/m2 이상으로 분류되고 있지만, 같은 수준의 BMI를 가진 개인이라도 같은 수준의 체지방률을 가지는 것은 아닐 수 있어 이는 대략적인 지침으로 간주되어야 한다고 설명하였다[13].
다양한 신장을 가진 개인의 체중을 서로 비교 가능하게 한 상대체중지수인 BMI는 현재 모든 대상에게 사용될 수 있는 비만척도 역할을 하고 있다. 하지만 상대체중지수의 본래 역할인 모든 성별, 연령, 신장을 아울러 체중을 표준화 할 수 있는 지수인지 고찰한 연구는 국내에 미비한 실정이다.
따라서 본 연구는 국민체력인증센터 체력측정 참여자의 자료들을 통해 한국인 성인 남녀의 체중을 표준화하기 가장 타당한 상대체중지수를 확인하고 BMI와 같이 체지방률 예측변인의 역할을 수행하기 적절한지 확인하는 것에 목적이 있다.
연구 방법
1. 연구 대상
본 연구는 한국인 남녀에게 적용하기 가장 적절한 상대체중지수를 확인하고자 한다. 표본추출은 국민체육진흥공단 산하의 국민체력인증센터에서 2017년 5월부터 2021년 5월까지 4년간 체력측정에 참여한 18-65세의 남성 183,751명, 여성 169,633명의 자료를 분석하였다. 연구대상 추출은 비확률 표본추출방법의 하나인 판단표본 추출방법을 통해 진행하였고 비정상적으로 크거나 작은 수치를 보이는 자료는 삭제하였다. 정상 혈압 범위를 과도하게 이탈하는 이완기 혈압 61-89 mmHg, 수축기 혈압 101-130 mmHg를 벗어나는 자료 또한 대사증후군의 영향을 받을 수 있다고 판단해 사전에 삭제하였고[14,15], 남성 77,705명, 여성 84,641명을 선정하여 이들에게서 수집된 신장, 체중, 체지방률 자료를 사용하였다. 대상자의 일반적 특성은 Table 1과 같다.
Table 1.
Subject characteristics
2. 측정 변인
1) 상대체중지수
본 연구에서 사용할 체질량지수는 체중/신장지수 [I1 =W (kg)/H (m)], BMI [I2 =W (kg)/H2 (m2)], PI [I3 =W (kg)/H3 (m3)]이며 추가적으로 선행연구[6]에서 상대체중지수로서 여성에게 더 타당함을 보인 W (kg)/H (m) 지수에 2를 나누어 표준 오차를 간단하게 줄인 [I4 =W (kg)/H (m)/2] 를 포함해 총 네 가지 지수를 사용하였다. 이는 전국의 국민체력인증센터에서 공통으로 사용되는 신장체중계(Inbody, Korea)를 통해 측정된 신장, 체중의 값을 사용하여 계산하였다.
3. 자료처리방법
통계적 자료 분석을 위해서 SPSS version 21을 사용하여 기술 통계량(Means±SD)을 산출하였다. 먼저 체중과 높은 상관, 신장과 낮은 상관을 보이는 지수를 확인하고 체지방률과 높은 상관을 보이는 지수를 확인하기 위해 Pearson’ s correlation 분석을 이용하여 알아보았다. 다음으로는 모든 연령, 신장의 범위에서 사용될 수 있는 상대체중지수를 확인하기 위해 다음과 같은 세 가지 방법을 사용하였다. 첫째, 각 상대체중지수가 모든 신장 범위에서 비슷한 수준의 표준체중을 나타내는지를 가시적으로 확인하기 위해 선형회귀분석을 실시한 후 비표준화계수의 베타값이 가장 낮은 지수를 확인하였고 그래프를 산출하였다. 둘째, 모든 신장 범위에서 지수의 평균값을 구한 후 산점도 그래프로 제시하였다. 셋째, 독립변인 신장과 종속변인 체중의 회귀분석을 실시하여 신장별 표준체중을 구하는 회귀방정식을 도출하였고 낮은 신장그룹과 높은 신장그룹의 상대체중지수인 W/H n을 같게 하는 지수 n의 값을 구하였다. 모든 자료의 통계적 유의수준은 α=.05로 설정하였다.
연구 결과
1. 한국인 성인 남성에게 가장 타당한 체질량지수
Table 2에서 제시한 바와 같이 18-65세 남성의 체중과 가장 높은 상관을 보이는 지수는 I1 (r=.973), 그 다음으로는 I2 (r=.880), I3 (r=.725)이었다. 신장과 낮은 상관을 보이는 지수는 I2 (r=-.009)였으며 I1, I3는 각 .250, -.268의 상관을 보였다.
Table 2.
Pearson correlation coefficients between Height, Weight, Indices I1, I2, I3, I4, %Body fat and Age in male
| Height (cm) | Weight (kg) | I1 (kg/m) | I2 (kg/m2) | I3 (kg/m3) | I4 (kg/m2) | Body fat (%) | |
|---|---|---|---|---|---|---|---|
| Weight (kg) | .463∗∗ | 1 | |||||
| I1 (kg/m) | .250∗∗ | .973∗∗ | 1 | ||||
| I2 (kg/m2) | -.009∗∗ | .880∗∗ | .965∗∗ | 1 | |||
| I3 (kg/m3) | -.268∗∗ | .725∗∗ | .863∗∗ | .965∗∗ | 1 | ||
| I4 (kg/m2) | .250∗∗ | .973∗∗ | 1.000∗∗ | .965∗∗ | .863∗∗ | 1 | |
| Body fat (%) | -.191∗∗ | .527∗∗ | .625∗∗ | .697∗∗ | .722∗∗ | .625∗∗ | 1 |
| Age (yr) | -.289∗∗ | 0 | .074∗∗ | .155∗∗ | .227∗∗ | .074∗∗ | .257∗∗ |
Table 3에는 독립변인 신장과 종속변인 상대체중지수에 대한 그래프의 기울기를 확인하기 위한 선형회귀분석의 결과이다. 비표준화계수가 0에 가까워 신장과 독립적인 지수는 I2 (B=-.005 p <.05)임을 확인할 수 있었고 결과에 대한 그래프는 Fig. 1의 좌측에 제시한 바와 같다. Fig. 1 우측에는 각 신장별로 분포한 지수의 평균값을 산점도로 제시하였다. Fig. 1의 결과 남성에게는 I2가 모든 신장 범위에서 같은 값의 표준체중을 제시하기 적합했다.
Fig. 1.
Fig. 1.(A) Simple linear regression line between height and indices in male. (B) Mean value of Indices on Height in male.
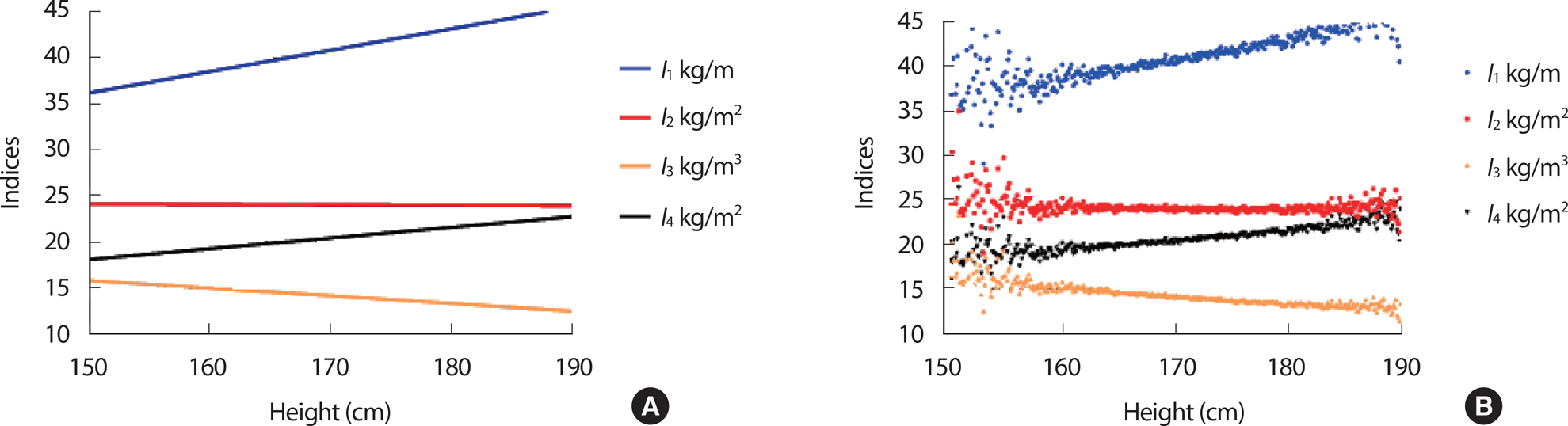
Table 3.
Results of simple linear regression analysis in male
Table 3에서 제시한 신장과 체중의 회귀분석결과 남성의 표준체중(Ŵ)공식은 Ŵ=0.82×신장-69.855이다. 남성의 평균신장을 기준으로 ±2표준편차를 낮은 신장집단 161 cm (H1), 높은 신장집단 185 cm (H2)이라고 가정하고 두 집단의 표준체중을 각 Ŵ1, Ŵ2라고 하였을 때, 상대체중지수 Ŵ1/H1n =Ŵ2/H2n가 성립해야 하며 이는 62.165/161 n = 81.845/185 n이다. n의 값은 (log81.845-log62.165)/(log185-log161)=1.98으로 남성의 경우 2를 지수로 갖는 I2 와 가장 가까운 것으로 나타났다.
2. 한국인 성인 여성에게 가장 타당한 체질량지수
Table 4에서 제시한 바와 같이 18-65세 여성의 체중과 가장 높은 상관을 보이는 지수는 I1 (r=.969), 그 다음으로는 I2 (r=.873), I3 (r=.736)이었다. 신장과 낮은 상관을 보이는 지수는 I1, I4 (r=-.049)가 가장 낮았으며 I2, I3는 각 -.250, -.424의 상관을 보였다.
Table 4.
Pearson correlation coefficients between Height, Weight, Indices I1, I2, I3, I4, %Body fat and Age in female
| Height | Weight | I1 (kg/m) | I2 (kg/m2) | I3 (kg/m3) | I4 (kg/m2) | Body fat (%) | |
|---|---|---|---|---|---|---|---|
| Weight (kg) | .293∗∗ | 1 | |||||
| I1 (kg/m) | .049∗∗ | .969∗∗ | 1 | ||||
| I2 (kg/m2) | -.205∗∗ | .873∗∗ | .967∗∗ | 1 | |||
| I3 (kg/m3) | -.424∗∗ | .736∗∗ | .881∗∗ | .973∗∗ | 1 | ||
| I4 (kg/m2) | .049∗∗ | .969∗∗ | 1.000∗∗ | .967∗∗ | .881∗∗ | 1 | |
| Body fat (%) | -.248∗∗ | .588∗∗ | .680∗∗ | .730∗∗ | .734∗∗ | .680∗∗ | 1 |
| Age (yr) | -.398∗∗ | .069∗∗ | .177∗∗ | .276∗∗ | .350∗∗ | .177∗∗ | .184∗∗ |
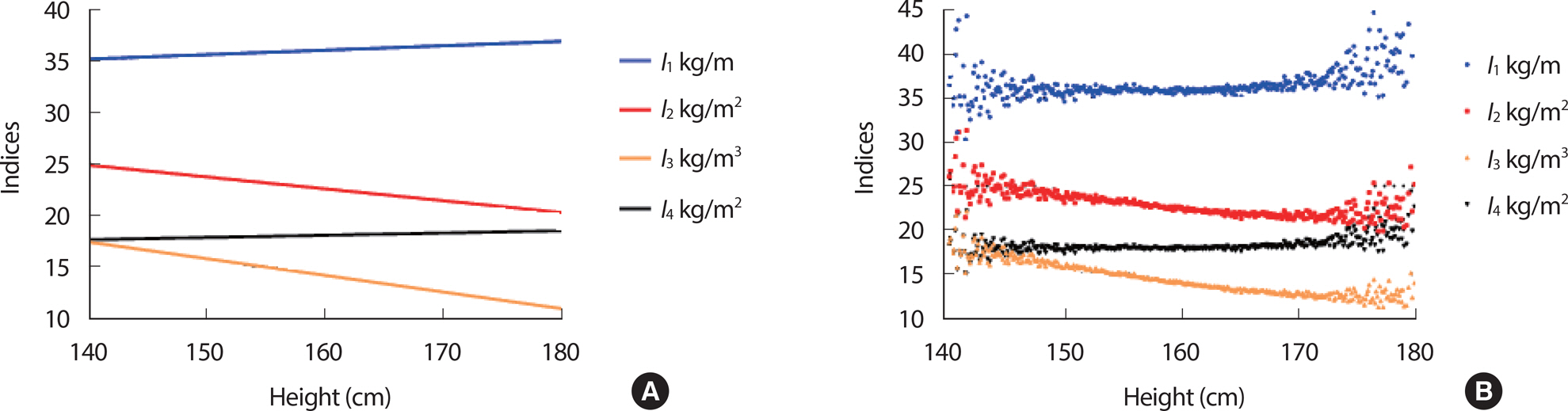
독립변인 신장과 종속변인 체질량지수에 대한 그래프의 기울기를 확인하기 위해 선형회귀분석을 실시한 결과는 Table 5에 제시한 바와 같다. 비표준화계수의 베타값이 0에 가까워 신장과 독립적인 지수는 I4 (β=0.022, p =.01)임을 확인할 수 있고, 그래프는 Fig. 2에서 제시한 바와 같다. Fig. 2 우측에는 각 신장별로 분포한 지수의 평균값을 산점도로 제시하였다. Fig. 2의 결과 여성에게는 I4가 모든 신장 범위에서 같은 값의 표준체중을 제시하기 적합했다.
Table 5.
Results of simple linear regression analysis in female
Table 5에서 제시한 신장과 체중의 회귀분석결과 여성의 표준체중(Ŵ)공식은 Ŵ=0.433×H-11.61이다. 여성의 평균신장을 기준으로 ±2표준편차를 낮은 신장집단 148 cm (H3), 높은 신장집단 172 cm (H4)이라고 가정하고 두 집단의 표준체중을 Ŵ3, Ŵ4라고 하였을 때, 상대체중지수 Ŵ3/H3n =Ŵ4/H4n가 성립해야 하며 이는 53.474/148 n =62.866/172 n 이다. 따라서 지수 n의 값은(log62.866-log53.474)/(log172-log148)=1.20으로 여성의 경우 1을 지수로 갖는 I1, I4 와 가장 가까운 것으로 나타났다.
Table 6은 여성의 특정 신장에서 나타내는 지수의 평균값에 대한 표이다. 각 지수의 평균값을 기준으로 오차의 범위가 가장 낮은 지수는 I4 지수임을 확인할 수 있다.
Table 6.
Indices at specified Heights of female aged 18-65
Table 7은 여성의 표준체중을 제시하기 적합한 상대체중지수인 I1, I4의 타당성을 확인하기 위해 실제 측정된 값과 근사치로 추정된 상대체중지수 값의 차이를 분석한 것이다. 추정된 상대체중지수의 표준편차를 계산하기 위해 비추정(Ratio estimation) 방법을 사용하였다.
Table 7.
Mean and standard deviation of I1, I4, computed by exact and ap proximate measurement
| I1 (kg/m) | I4 (kg/m2) | ||
|---|---|---|---|
| Exact measurement | Mean (ΣW/H/n) | 36.04 | 18.02 |
| SD | 5.08 | 2.54 | |
| Approximate measurement | Mean (W/H) | 36.09 | 18.04 |
| SD | 5.08 | 2.54 |
Table 1과 Table 4에 제시된 W(평균체중), H(평균신장), Sw(체중의 표준편차), Sh(신장의 표준편차), r wh(신장과 체중의 상관관계)를 이용해 추정값의 표준편차를 계산하는 공식은
Fig. 2.
Fig. 2.(A) Simple linear regression line between height and indices in female. (B) Mean value of Indices on Height in female.
이며 I4의 표준편차는 위 공식에 2를 나누면 구할 수 있다. 분석결과 직접 측정된 수치와 추정된 수치가 매우 일치하는 것을 확인할 수 있었다.
논 의
1. 상대체중지수
1832년 Quetelet의 BMI 지수, 1897년 Ponderal 지수, 1921년 로러지수가 제안되었고, 20세기 중반, 가장 많이 사용되는 지수는 W/H, W/H2, W/H3가 되었다. 이중 W/H2인 Quetelet의 BMI 지수가 체중과 높은 상관을 보이고 신장의 차이로부터 독립적이기 때문에 덜 편향적이라는 관점에서 가장 적절한 지수로 여겨졌고[8], 서양 여성에서는 W/H 지수가 더 적절할 가능성이 있다는 의견이 제시되었다[16].
BMI는 비만과 과체중 판정의 척도로 유용하게 사용되고 있지만 개인의 체지방량을 정확히 반영하지 못하기 때문에 비만진단의 표준방법(gold standard)이 되기 어렵고[11,17], BMI를 통해 개인의 체지방을 추정하는 것은 개인차가 크기 때문에 비만척도로 사용할 때에는 신중하게 사용되어야 한다는 연구결과들이 발표되었다[18]. 따라서 본 연구는 상대체중지수의 비만판정척도의 역할보다 신장이 다른 개인 간의 체중비교를 가능하게 하는 지수로서의 역할을 중점으로 논의하고자 한다.
선행연구의[7] 의견과 같이 표준체중 판정을 위한 상대체중지수는 체중과 상관이 높고, 신장과 상관이 낮아야 한다. 이는 150 cm, 180 cm 의 키를 가진 두 개인이 표준체중을 갖는다면 같은 값의 지수를 가져야 하기 때문이다. 남성과 여성의 체중과 지수, 신장과 지수의 상관관계분석 결과 남성의 경우 I2, 여성의 경우 I1, I4가 표준체중 판정을 위한 지수로 가장 타당함을 확인할 수 있었다. 또한 회귀분석 결과 제시되는 그래프가 모든 신장 범위에서 일정한 값을 가져야 하므로, 신장과 상대체중지수의 선형회귀분석 결과 제시되는 비표준화계수의 베타값이 0에 가까워야 하고, 신장과 상대체중지수의 평균 간 산점도 그래프 결과가 그래프의 x축과 평행에 가까워야 낮은 신장집단과 높은 신장 집단에서 모두 사용할 수 있는 지수 조건을 만족한다. 남성과 여성의 신장과 상대체중지수들 간의 선형회귀분석 결과 남성의 경우 I2, 여성의 경우 I4의 비표준화계수 베타값이 가장 낮았다. 신장별 지수들의 평균값 산점도 또한 남성의 경우 I2, 여성의 경우 I4가 그래프의 x축과 가장 평행하는 양상을 보여 모든 신장범위에서 공히 사용될 수 있는 표준체중지수로서 가장 타당함을 확인할 수 있다.
신장과 체중의 회귀분석 결과의 표준체중공식을 이용해 모든 신장 범위에서 사용할 수 있는 상대체중지수인 W/H n의 n값을 구하는 방법은 Khosla & Lowe [7]의 20-24세를 대상으로 한 이론적 접근방법을 참고하여 이를 18-65세 남녀로 확장시킨 것으로 남성의 경우 W/H1.98 (≈ I2), 여성의 경우 W/H1.2 (≈ I1, I4)일 때 가장 정확히 상대체중지수의 역할을 할 수 있을 것으로 생각된다. 이는 Florey [6]와 Lee et al. [19]의 연구에서 남성집단은 I2, 여성집단은 I1이 상대체중지수로서 가장 적합할 가능성이 있다고 결과를 제시한 것과 같다.
Khosla & Lowe [7]는 실제 측정된 상대체중지수와 근사치로 추정된 상대체중지수의 차이를 비추정(Ratio estimation)을 통해 비교하여 신장과 낮은 상관을 보이고 체중과 높은 상관을 보이는 지수의 타당성을 확인하였다[20]. 본 연구결과 여성에게 표준체중을 제시하기 적절했던 I1, I4를 지수로 사용하기 타당한지 확인하기 위해 기존에 Khosla & Lowe의 연구에서 사용되었던 근사치로 추정된 I2의 표준편차를 구하는 공식을 I1, I4에 사용할 수 있도록 수정하여 비추정 방법을 사용하였고[21], 선행연구와 동일하게 두 값의 평균과 표준편차가 큰 차이를 보이지 않아 여성의 체중비를 비교하는 지수로 사용되기 타당한 것으로 생각된다.
Buss [11]에 의하면 BMI는 성별, 인종, 연령대에 걸쳐 동등하게 타당하지 않을 수 있으며, 본 연구결과 현재 여성에게 사용되는 BMI는 신장과의 역상관(r=-.205)을 보이기 때문에 신장이 높아질수록 표준체중 값이 낮아지는 양상을 보인다. 따라서 여성에게 BMI를 사용할 경우 신장별로 다른 준거를 적용할 필요가 있을 것이다. 이는 Lee et al. [19]의 연구에서 전통적인 지수들 중 모든 성별, 신장에서 쓰일 수 있는 지수는 없었다는 연구결과와도 같다. 따라서 본 연구결과는 성별별로 다른 상대체중지수를 사용해야 할 필요가 있음을 시사하는 바이며, 상대체중지수 계산의 평이성과 보편성을 고려하였을 때[22] I1에서 2를 나눈 I4는 신장이 다른 개인 간 지수의 표준오차를 간단하게 감소시키는 역할을 해 여성의 경우 I4를 사용하여 상대체중을 평가하는 것이 더욱 적절하다고 생각된다.
2. 체지방률
Dembert et al. [23]은 20-42세 미 해군 잠수부 남성에서, BMI가 신장과 가장 낮은 상관을 보이고 체지방률과 높은 상관을 보이기 때문에 비만의 가장 간편한 예측변인라고 하였다. Choi et al. [24]의 304명의 여자 대학생을 대상으로 한 BMI 지수와 Ponderal 지수의 타당성 검증 논문에서는 신장과의 상관을 배제시키지 않는 선형모양의 체중비 추정을 위해 Ponderal 지수의 활용 가능성을 제시한 바 있다. 하지만 본 연구결과에서는 BMI 지수와 Ponderal 지수 모두 체지방률과 비슷한 수준의 상관관계를 보이며, 신장과의 상관을 배제시키지 않는 Ponderal 지수를 사용할 경우 신장이 다른 두 개인에게 다른 비만 판정 준거를 적용해야 한다는 불편함이 있기 때문에 일상 속에서 편리하게 사용하기엔 적절하지 않을 것으로 판단된다.
결 론
본 연구는 국민체력인증센터에서 체력측정에 참여한 18-65세의 남성 77,705명, 여성 84,641명의 신장과 체중, 체지방률 정보를 사용하여 상대체중지수로 사용하기 가장 타당한 지수를 확인하고 체지방률을 예측하기 위한 예측변인의 역할을 수행할 수 있는지 확인하기 위해 진행되었다. 한국인 18-65세 남성의 경우, 모든 신장의 범위에서 사용하기 가장 적절한 지수는 기존의 BMI로 알려진 W (kg)/H2 (m2)였고, 여성의 경우 W (kg)/H (m) 혹은 간단하게 표준오차를 줄인 W (kg)/H (m)/2 지수였다. 따라서 한국인 성인 남성은 24.0 kg/m2 성인 여성의 경우 18.0 kg/m2를 표준체중으로 설정하여 개인 간 상대 비교를 하는 것이 적합할 것이라고 생각되며 여성의 경우 새로운 비만판정 분류 준거를 마련하기 위한 후속연구가 필요할 것으로 생각된다. 모든 상대체중지수에서 체지방률을 추정하기에 부족했지만 두 성별 모두 Ponderal index인 W (kg)/H3 (m3)에서 체지방률과 가장 높은 상관을 보였고, 이는 후속연구에서 상대체중지수를 이용하여 체지방률을 추정하기 위한 연구의 예측변인으로 사용되기 적절할 것으로 생각된다.





