골노화 요소 기반 생물학적 나이 예측모델개발 및 낙상과 보행에 따른 생물학적 나이
Development of Biological Age Prediction Model Based on the Osseous Parameters and the Effects of Endurance Exercise Duration and Falling on Aging
Article information
Trans Abstract
PURPOSE:
The aims of this study were to identify bone health related biomarkers, develop an osseous health based biological age (BA) prediction model, and investigate its applicability.
METHODS:
Data of a total of 4,644 eligible male participants (age≥30 years) examined for bone health from the 2010 and 2008 Korea National Health and Nutrition Examination Survey were used in the study. Among 15 bone health related variables, 5 biomarkers were selected through a parsimonious exclusion procedure and correlation analysis between the parameters and chronological age. Principal component analysis was applied to extract the principal component factors. Through application of CA and adjustment procedure, a BA prediction model based on osseous biomarkers was obtained. Applicability of the model was assessed. First, history of fall was compared between the fall and no-fall groups. Second, three groups were compared for their continuous walking durations. All groups were compared by three age groups.
RESULTS:
BA was significantly greater than CA in the fall group by 5.60 years for the older group. As for the walking duration, BA was significantly less by 5.14 and more by 6.51 years than CA for the older groups with more than 2 hours and less than 1 hour of walking durations, respectively.
CONCLUSIONS:
BA prediction model based on five non-invasive osseous biomarkers may be applicable to predict bone health related conditions. It may be used as a health promotional tool in a health related field to deter or even reverse health deterring factors.
Introduction
Aging of an individual can vary depending of various internal and external factors. Despite the rapid growth in field of science and technology, the exact mechanism of aging is still in the mist. More than 300 theories exist that explain the aging phenomenon with different perspectives [1,2]. Grossly viewed, there may be an infinite number of perspectives on aging since different species have different aging rates and patterns. For example, some specifies such as tortoise and many other reptiles decrease or remain the same as they age [2]. With humans, the morality rate increases exponentially with increasing age. It has been a fundamental quest for many scientists to deter or reverse the aging process for better longevity and extended life for centuries. However, despite the efforts invested in the quest for everlasting youth, aging still is a natural phenomenon that cannot be influenced by external manipulation. Although external manipulation may not alter the genetic composition and extend expected life span, influencing exogenous and endogenous factors to some extend may deter the expedited aging process up to certain level. For example, free radical and reactive oxygen specifies (ROS) have been known to increase the damage biologically significant targets with oxidative stress for accelerated aging [3]. In addition, numerous tests are available to predict clinically problematic conditions to deter or eliminate further progression of the adverse conditions. Predicting the possibility of disease onset and progression has helped humans to live their expected lifespan to the fullest.
With different internal and external influencing factors for aging, a different concept of aging has been suggested to differentiate between the age calculated by the passing time and the age calculated by the deterioration rate of different sectors of human physiology. The age calculated by the elapsed time since the birth is called the Chronological age (CA). CA merely informs the health status of the majority of population at certain stage in elapsed time. It does not inform specific state of an individual. Although the normal developmental phases and rates can be calculated by simple mathematics, the rate of physiological decline cannot be clearly estimated by CA [4,5]. The physiological aging process is an individually uniquely process where multivariate factors influence the outcome. The concept of biological age (BA) was proposed to estimate the gradual functional and structural deterioration of an individual [5-7].
Numerous scientists have focused their research goal on estimating accurate BA for decades [6,8]. Several BA estimating models have been reported to estimate BA of individuals with various biomarkers. Since multivariate factors such as genetic, physiological, and psychological factors may be involved in the aging process, different sets of biomarkers have been used to estimate BA [9-13]. A few groups of biomarkers with specific characteristics have been contemplated to represent the progressive state of individuals in comparison to their CA. The groups of biomarkers have been composed of either physical, biochemical, hormonal, or physiological parameters [4,14,15].
The biomarkers of BA have been selected based on the correlation with CA. Since the concept of BA was proposed to provide reliable estimation of deterioration in a general population, a set of biomarkers should change in function of CA. Although previous BA estimation models with specific groups of biomarkers showed correlation with CA, they could not present all corners of the deterioration state. Therefore, different sets of biomarkers seem necessary to represent the deterioration rate or BA of specific health state. As there is increasing evidence of bone health and aging, BA model should be based on osseous parameters. Bone loss with advancing age has been known to threaten loss of independence and health [16,17].
The BA prediction models have been used in the clinical environment as a health promotional tool to provide clinical information by comparing the health status of an individual with CA and the general population. Therefore, commonly assessed bone health related parameters were used to select biomarkers and develop a BA prediction model. In addition, tedious inclusion and elimination steps provided by previous studies were applied to obtain accuracy in assessment and diagnosis [4,12,18,19]. In addition, the BA prediction model developed with osseous parameters were tested for its applicability by comparing two parameters, the regularly performed walking duration and fall experience. First, three groups of participants were selected based on their walking duration (less than 1 hour, between 1 and 2 hours, and more than 2 hours) to calculate and compare BAs between the groups. Second, two groups of participants were selected based on their fall experience to calculate and compare BAs between the groups. These groups were further subdivided by three age groups to thoroughly observe the deteriorating effects of aging.
Since a working prediction model needs to representative of a general population, this epidemiological research was conducted in a large-scale cross-sectional study at a population level using the fourth and fifth Korean National Health and Nutrition Examination Survey (KNHANES) data, adjusting for relevant covariates in selecting osseous aging biomarkers and associated BA prediction model. The goals of this study were to (a) obtain a set of osseous biomarkers from a group of participants that represents the Korean population, (b) develop an osseous BA prediction model through thoroughly selected biomarkers, (c) apply the BA prediction model to a group of individuals with previous history of fall and walking habit to predict and compare BAs.
Materials and Methods
Participants
Data of a total of 4,644 eligible male participants (age ≥ 30 years) from the fourth and fifth KNHANES which included the health behavior questionnaires, anthropometric, and osseous health measurements were utilized for the study. The fifth and fourth KNHANES assessment data of 2010 and 2008 were approved by the ethics committee of the Korea Centers for Disease Control and Prevention (IRB approval no: 2010-02 CON-21-C and 2008-04EXP-01-C).
The examination results from 1,318 male participants aged 30 and older with mean and standard deviation (SD) of 50.42 (13.59) were finally selected from 2,334 participants of the fifth KNHANES data. Significant decline in the physiological state and function were reported from the CA of 30 [4,20]. Following osseous parameters were used for the study: bone mineral densities of 15 area, femur trochanter, femur intertrochanter, femoral neck, Ward’s triangle, 1st through 4th lumbar spines (L1-4), left and right arm, pelvic, left and right leg, and left and right coastal bones (g/cm2) measured by DXA (Hologic Discovery, Hologic Inc., Bedford, MA, USA), were obtained. The machine was calibrated daily, and the coefficients for duplicate measurements were obtained regularly to maintain its reliability. In addition, 4,644 participants of the fourth KNHANES data for the BA prediction model assessment. Covariant factors which may influence of osseous health such as recent traumatic event such as fracture, vigorous and moderate exercise habits, and BMI (body mass index) were considered and excluded from the initially selected participants. 595 participants were selected for the final analysis.
Statistical analysis
Stratified cluster sampling and weighted values were applied to a nationally representative sample by the KHANES. The data were presented as mean±SD. In order to select the statistically significant biomarkers of aging, the Pearson correlation coefficient was calculated to examine the linear relationship between age and each parameter. Multiple regression models were used for building prediction models of BA. Variance inflation factors (VIF) which measure the impact of collinearity among the variables in a regression model were calculated for the selected biomarkers prior to building the BA prediction model. The fitness of the model was analyzed by calculating coefficient of determination (R2). All statistical data analyses were performed using the Statistical Package for the Social Sciences SPSS 20.0 software. In order to observe the statistically significant difference between BA and CA, one-way analysis of variance (ANOVA) was conducted and followed by for Bonferroni post-hoc analysis. Statistical significance was obtainedif p< .05.
Biomarker selection criteria and exclusion procedure
Selected biomarkers were first tested for multicollinearity. The results showed that all 5 variables were below the VIF cutoff point of 10 with 2.27 as the largest VIF observed Table 1 [21]. VIF greater than 4 may suggest concern for multicollinearity [22]. Selecting the right variables for BA estimation is second to none in developing a reliable prediction model. First, all the outliers above and below 1 percentile (mean±3 SD) of the normal distribution ranges were first sorted out prior to the exclusion procedure [4]. Second, the participants were prescreened for bone metabolism related disease such as hyperthyroidism, hyperparathyroidism, chronic renal failure, bronchial asthma, degenerative and rheumatoid arthritis, osteoporosis, and cancer based on the assessment and interview results conducted by medical specialists [23,24]. Furthermore, all participants diagnosed of osteoporosis (T-score ≤-2.5) were excluded [24]. Osteoporosis is defined as a BMD of -2.5 SD below the peak bone mass of a young, healthy, gender- and race-matched reference [23].
After the initial exclusion steps, the Pearson’s correlation coefficient analyses were conducted between the osseous parameters and CA. The parameters with correlation coefficients below .15 (p< .01) were excluded [4]. Six parameters of 1,318 participants remained after the correlation analysis. Five parameters remained after the redundancy analysis. Finally, principal component analysis was conducted with 5 parameters to conduct a structural relationship assessment by loading and unloading CAs to the parameters [4,25]. Therefore, a total of the remaining 5 parameters were selected as osseous biomarkers (Table 1).
Results
Construction of the prediction models
Principal component analysis (PCA) is a popular BA estimation algorithm which determines a covariant structure through an orthogonal transformation. The PCA statistical method incorporates multiple linear regression approach to form a single estimation algorithm [4,13,19]. The PCA method combined all parameters to form one principal component with eigenvalue and percent variation of 3.21 and 64.19%, respectively. The principal component and the candidate biomarkers were tested for their stability by loading and unloading the CA values to the analysis. After testing for the stability, the BA scores were calculated. The BA scores were obtained through the multiple linear regression analysis between the first principal components and the biomarkers. The BA scores were then modified to represent the scores similar to that of CA by adding the CA values into the formula [4,26]. The initial formula was further modified by adjusting for the under- and over-estimated BAs. Ages of some individuals have been reported to deviate from the mean of the population due systemic errors [9,25]. Such systemic errors were corrected by adding z scores (difference between the individual CA and the mean CA multiplied by 1 minus b) to the BA values. Following BA prediction model was derived after the final adjustment.
BA=159.554–22.72×Ward–23.47×L2–52.04×Arm–24.84×Plv–25.91×Leg+.61×CA (1)
The linear relationships between BA and CA were expressed in terms of coefficients of determination (R2 =.55, p< .001) and slope of the regression line was .78 (Fig. 1). The groups were further three differentage groups for the closeness between BA and CA: young group (YG =30 ≤ CA <45), middle-aged group (MG = 45 ≤ CA <65), and older group (OG = 65 ≤ CA). The regression slopes were .42, .45, and .42 for YG, MG, and OG, respectively.
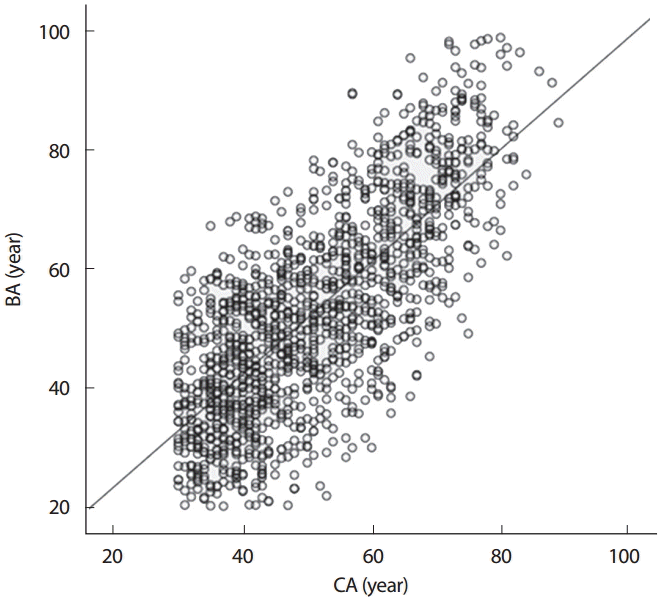
Biological age (BA) plotted in function of chronological age (CA) with the osseous based BA prediction model.
Assessing the usability of the developed BA prediction model is essential for possible clinical application. Therefore, two groups of participants were selected from the fourth KNHANES data for comparative analysis. Questionnaires on the previous history of fall and walking habit by continuous walking duration were used to select participants. CA and BA were calculated for all ages and by three age groups. Since the aging rate change with the progression of CA, the groups were divided into three age groups: younger, middle-aged, and older groups as in previous studies [9,19]. First, the BA prediction model was applied to a group of participants to calculate and compare BA between the fall and non-fall groups (Table 2). The CA and BA differences were calculated for each group to observe the effects of osseous health on the fall changes. Although significant differences were not observed between all age groups, BA of the fall group (-1.96 years) was lower than the non-fall group (1.66 years). BA changes were further observed for different age groups: YG, MG, and OG. Greater average BAs were shown for the fall groups of MG, and OG by 2.02 and 5.60 years, respectively. On the other hand, the average BAs were less for the non-fall groups of YG and MG by 3.14 and 2.24 years, respectively.

Differences in chronological age and biological age in three age groups with and without history of fall within one year
Regularly performed physical activity was also observed for the influence on BA (Table 3). Three groups were divided according to the continuously performed walking duration (WD): WD less than 60 minutes; WD more than 60 minutes and less than 120 minutes; WD greater than 120 minutes. Significant difference of 6.51 years was observed for OG with less than 1 hour of continuous walking duration. In addition, although significance was not observed, BA of OG with more than 2 hours of walking duration was less than CA by 5.14 years.
Discussion
Cells in human body are genetically programmed for uniquely specific life spans. Such specific life spans can also be influenced by both avoidable and unavoidable external factors. Therefore, it may be difficult to develop a universally fitting BA prediction model that could estimate BA for all health conditions. Different BA estimation models with uniquely specific biomarkers may be needed to predict more specific BAs of different physiological health. However, a common goal of the BA prediction models would be to elucidate the rate of deterioration for an individual. Currently, the best suggested way is to compare such deterring rates with normal individuals within a genetically homogeneous population using a specific prediction model for particular state of health. Therefore, this study obtained osseous biomarkers from a representative group of Korean male population to develop a BA prediction model. Five osseous biomarkers were selected through a thorough parsimonious step-by-step exclusion and inclusion criteria process. Each biomarker was bone mineral density (BMD) derived from different parts of the body: arm, leg, spine, pelvic, and hip (ward’s triangle). Developed osseous biomarker based BA (equation 1) was tested for its applicability with two different state of heath: fall experience and continuous walking duration.
Some of the osseous biomarkers found in this study were previously reported to be associated with the aging progression. The Ward’s triangle is the area commonly measured for osteoporosis. This area was shown to be the most negatively associated location in function of increased CA. Ward’s triangle is the radiolucent area formed near the center of femoral neck by the intersection of tree trabecular bundles [27]. Initial bone loss in the femoral neck is markedly observed in this area [27]. Three out of five osseous biomarkers are from the lower extremities. Two most common osteoporosis measurement sites are hip or proximal femoral neck and lumbar spine [28]. In this study, two additional bone locations were negatively increased in function of CA: the arm and leg. Wrist and upper arm fracture Weight-bearing has been known to plays a role in the bone mineral content of the lower extremity. There have been studies that suggested muscle strength and body composition as clinical indicators of osteoporosis. Reductions in body weight and muscle strength have been known to reduce bone mineral contents of the lower and upper extremities [29].
The correlating relationship of the developed BA estimation model based on the osseous biomarkers with CA was .74 (R2 =.55). Previously reported correlation coefficients for the BA prediction models ranged from .67 and .82 [4,13]. Compared to previous results, developed BA estimation model was rather reliable. The model showed similar fitness of the BAs toward the mean BA values. Such centralized fitness was also shown by the slopes and figures of YG, MG, and OG in function of CA for the other models [4,9,19,25]. In addition, the initial study group for the development of BA estimation model is composed of a wide range of participants with different ages – from 30 to 89. The rate of deterioration has been known to increase with the increased in CA. Calculating BA for different age groups as one group should either under- or over-estimate BA for different individual. Therefore, the observational groups were divided into YG, MG, and OG to consider the differences regression slop and to reduce possible error in calculation.
The applicability or usefulness of the estimation model can be tested through examination of certain health-related condition. The relationship between bone mineral density and osteoporotic fracture has been reported by numerous studies [30]. Moreover, fall history has been reported to be an independent risk factor for fracture. Fall frequency has been associated with increased fracture and low mineral density since some of the significant risk factors to fall are poor balance, muscle strength, and muscle power in the lower extremities [31,32]. Therefore, fall history was used to calculate and compare BAs for two groups of participants. First group or the fall group was composed of participants who reported more than or equal to 1 fall incidence in the last year. The other no-fall group was composed of participant who reported no history of fall in the last one year. The groups were first compared and further divided into three age groups for more detailed findings. The within the fall group, the older group (OG) showed the largest difference between CA and BA. The results indicate that the risk of fall increase with poor skeletal integrity, muscular performance, and dynamic balance in the elderly [31]. However, since the fall history is not a direct indication of bone health or deterioration status, regularly performed endurance exercise or continuous walking duration in minute was used to test the osseous based BA prediction model. Many studies have reported that aerobic endurance exercise is positively related to the bone health since regularly performed weight-bearing exercises significantly enhance and maintain bone mineral content [33,34]. In addition, the foot muscle coordination is improved during walk for the prevention of fall. The comparative results of this study showed very interesting results. Although the walking duration had minor influence on BA for all age groups in YG and MG, increased walking duration of 2 hours or more significantly increased BA by 5.14 years in the OG. In addition, walking less than 1 hour significantly increased BA by 6.51 years. The BA difference between walking duration less than 1 hour and more than 2 hours was about 11 years, indicating strong influence of walking in bone health in the older group. Although not shown in the result section, the BA difference was as much as 20 years between several fall and non-fall individuals older than 80 years of age. It has been widely accepted that aging and inactivity significant accelerate lowering of bone mineral contents in the elderly. Therefore, increase in BA composed of osseous biomarkers should not be surprising for the older group [35]. The results indicated that regularly performed endurance exercise such as walking deters bone degradation and even improve bone health.
Many investigators suggest that a valid set of biomarkers should consist of parameters representing function. The osseous parameters are non-invasive variables commonly and nationally tested across the Korean male population. The study has limitation that not all the sites for identifying osteoporosis are tested in this nationally tested health exams. Additional measurement sites should be included in the future studies to elucidate the most age correlating sites.
Conclusion
A battery composed of five osseous parameters or biomarkers was obtained through thoroughly conducted exclusion and inclusion procedure. These biomarkers went through several statistical steps to for a BA prediction model for bone health assessment. This non-invasive BA prediction model may be used as a guidance tool in a health related center to address and advocate bone health on an individual based. Developed BA model was tested for its applicability in two different bone related problems: fall history and walking duration. Both tests indicated that fall history and sedentary life style were all effective in increasing BA especially for the older group. Therefore, osseous parameters may be used to inform bone health status.

